Genetic Algorithm (MATLAB)

Aim :

      write a code optimise the salagmite function and find the global maxima of the function in MATLAB.

Objective :

• Explaination about genetic algorithm and syntax of ga function.
• write the salagmite function to find the global maxima in matlab.
• write a progarm for plot F maximum vs no.of iterations of each studys.

Theory :

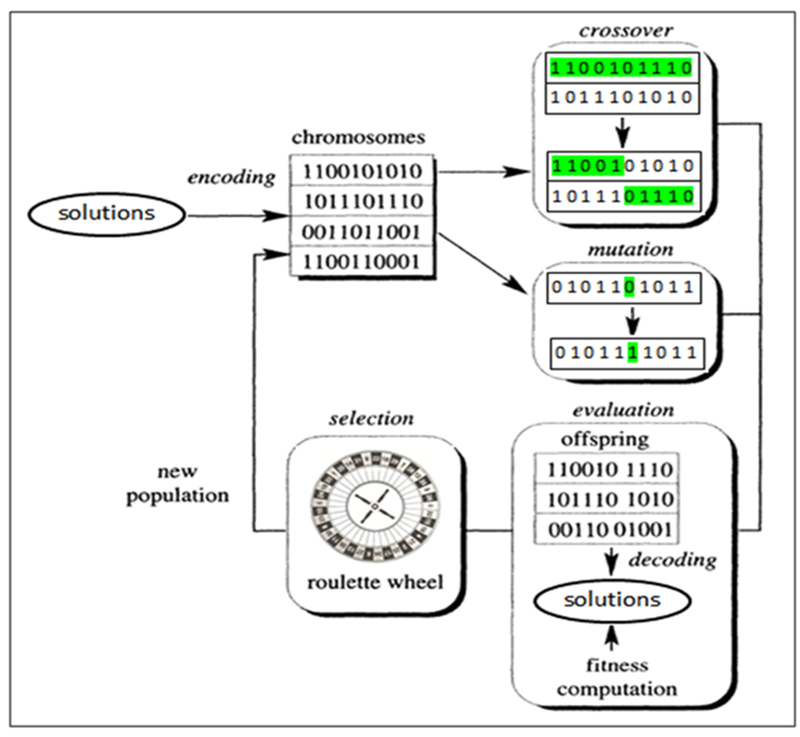
Genetic Algorithm :

     The genetic aldorithm is a method for solving both constrained and unconstrained optimization problems that is based on the natural selection, the process that drives biological evalution. The genetic algorithm repeatedly modifies a population of individual solutions. At each step, the genetic algorithm selects individuals from the current population to be parents and uses them to produce the children for the next generation. Over sucessive generations, the population "evolves" toward an optimal solution.

You can apply the genetic algorithm to solve a variety of optimization problems that are not well suited for standard optimization algorithm, including problems in which the objective function is discontinuous, nondifferentiable, stochastic, or highly nonlinear. The genetic algorithm can address problems of mixed integer programming, where some components are restricted to be integer-valued.

     This flow chart outlines the main algorithmic steps.

The genetic algorithm uses three main types of rules at each step to create the next generation from the current population :

• Selection rules select the individuals, called parents that contribute to the population at the next generation. The selection is generally stochastic, and depend on the individuals scores.
• Crossover rules combine two parents to form children for the next generation.
• Mutation rules apply random changes to individual parents to form children.

Syntax of 'ga' function :

This are the some of syntax of 'ga' function,

    1)  x = ga(fun,nvars)

 here, 

          x     = local minimum

         fun   = function

        nvars = number of design varibles

This finds the local unconstrained minimum (x) to the objective function (fun) for the dimension (nvars) of the function.

    2) x = ga(fun,nvars,A,b)

here,

       A = Linear inequalities

       b = Linear inequalities

    3) x = ga(fun,nvars,A,b,Aeq,beq)

here, 

         Aeq = Linear equalities

         beq = Linear equalities

set A=[] and b=[] if no linear inequalities exist.

    4) x = ga(fun,nvars,A,b,Aeq,beq,lb,ub)

here,

         lb = lower bound condition

        ub = upper bound condition

set Aeq=[] and beq=[] if no linear equalities exist.

    5) x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon)

here,

        nonlcon = Representing the nonlinear inequalities and equalities respectively

    6) x = ga(fun,nvars,A,b,Aeq,beq,lb,ub,nonlcon,option)

here,

       options = use as optimization to find global maximum.

Salagmite Function :

Program for Salagmite Function :

function [ f ] = stalagmite( input_vector )
a=input_vector(1); % inputs
b=input_vector(2);
term1=(sin((5.1*pi*a)+0.5))^6;               % Equation of f1_x
term2=exp((-4)*log(2)*((a-0.0667)^2)/0.64);  % Equation of f1_y
term3=(sin((5.1*pi*b)+0.5))^6;               % Equation of f2_x
term4=exp((-4)*log(2)*((b-0.0667)^2)/0.64);  % Equation of f2_y
[f]=-(term1*term2*term3*term4);          %inverts the objective function
end

Program for Genetic Algotithm :

%Genetic algorithm 
clear all 
close all 
clc
 %independent variacles 
x=linspace(0,0.6,150); 
y=linspace(0,0.6,150);
% matrix 
[xx,yy]=meshgrid(x,y);
%Number of iterations 
num_cases=50; 

% starting the loop 
for i=1:length(xx) 
   for j=1:length(yy) 
        input_vector(1)=xx(i,j); 
        input_vector(2)=yy(i,j); 
        f(i,j)=stalagmite(input_vector);
    end
end

%creates a three dimensional surface 
figure(1) 
surfc(xx,yy,-f)     %creates a surface to visualise 3D
shading interp      %Makes the surface look more smoother
xlabel('x value') 
ylabel('y value') 
title('Stalagmite Function') 

%study 1 : statistical behaviour of unbound condition input
tic
for i=1:num_cases 
     [inputs,fopt(i)]=ga(@stalagmite,2); 
     xopt(i)=inputs(1); 
     yopt(i)=inputs(2);
end 
study_1=toc %gives the time taken for study_1

figure(2)
subplot(2,1,1) 
hold on 
surfc(x,y,-f) %creates a surface to visualise 3D
title('Unbounded inputs') 
xlabel('x value') 
ylabel('y value') 
shading interp 
hold on 
plot3(xopt,yopt,-fopt,'marker','o','markersize',5,'markerfacecolor','r') 
subplot(2,1,2) 
plot(-fopt) 
xlabel('iterations') 
ylabel('function maximum') 

% study 2 : statistical behaviour of Bounded input (with upper and lower bounds) 
tic; 
for i=1:num_cases 
      [inputs,fopt(i)]=ga(@stalagmite,2,[],[],[],[],[0;0],[0.6;0.6]); 
       xopt(i)=inputs(1); 
       yopt(i)=inputs(2); 
end 
study_2_time=toc %gives the time taken for study_2

figure(3) 
subplot(2,1,1) 
surfc(x,y,-f) %creates a surface to visualise 3D
shading interp 
title('Bounded inputs') 
xlabel('x value') 
ylabel('y value') 
hold on 
plot3(xopt,yopt,-fopt,'marker','o','markersize',5,'markerfacecolor','r') 
subplot(2,1,2) 
plot(-fopt) 
xlabel('iterations') 
ylabel('function maximum') 

%study 3 : Increasing the population size 
% by doing so we are increasing the probability of the function 
% to canverge at global maximum 
options=optimoptions(@ga);
options=optimoptions(@ga,'PopulationSize',500); 

tic 
for i=1:num_cases 
      [inputs,fopt(i)]=ga(@stalagmite,2,[],[],[],[],[0;0],[0.6;0.6],[],[],options);  
      xopt(i)=inputs(1); 
      yopt(i)=inputs(2); 
end 

study_3_time=toc %gives the time taken for study_3

figure(4)
subplot(2,1,1) 
surfc(x,y,-f) %creates a surface to visualise 3D 
shading interp 
title('bounded inputs with increased population size') 
xlabel('x value') 
ylabel('y value') 
hold on 
plot3(xopt,yopt,-fopt,'marker','o','markersize',4,'markerfacecolor','r') 
subplot(2,1,2) 
plot(-fopt) %plotting -f vs number of iterations 
xlabel('iterations') 
ylabel('function maximum')

 Code Explanation :

      1) first step is clear all old data and graphs in command box and workspace by using clear all, close all, clc commands.

      2) create x, y vectors by using linspace command. and mesh this x and y values to get combination of the value (xx, yy) use meshgrid command.

     3) next step is to give number of iteration value by give (num_case=50) 50 time iteration will happen.

     4) create the loop for create salagmite function 3d surface using for loop and salagmite function which is above.

     5) create 3 dimensional surface surf() command and make look the surface more smooter we use shading interp command.

     6) and using xlable, ylable, title commands give the axis name and title to the 3d plot.

     7) after create this 3d surface the study 1 performed for statistical behaviour of unbound condition inputs by code  and tic and toc commands used for claculate the time for this study 1.

     8) then study 2 performed for satistical behaviour of bounded inputs. by giving [0,0][0.6,0.6] in the ga function where 0 is the lower bound and 0.6 is upper bound condition.

     9) then study 3 performed for satistical behaviour of bounded inputs by increasing population size using options. by giving [0,0][0.6,0.6] in the ga function where 0 is the lower bound and 0.6 is upper bound condition.

Outputs :

Salagmite Function :

Study 1 : Unbounded inputs :

        For our first study we will ues the for loop and iteration as 50 times use following syntax

[input,fopt]=ga(function,number of variables)

here, the number of variables are 2 that is x and y. This inputs can be stored and we can use the surf command to create a surface to visualize the function.

we can also use the marker command to find the points of local maximum. And tic, toc commands used to look at the time taken for evaluation.

So, the drawback of this study is that since ga command does not know the bounds of these x and y values. so, it can take the values greater than 0.6 or less than 0. so, to overcome this we need to set up a second study.

Time taken for study 1 :

Study 2 : Bounded inputs :

In the study 2 we setup upper and lower bounds for this ga function and the syntax is

[input,fopt]=ga(function,number of variables,A,b,Aeq,beq,lb,ub)

Where, lb is lower bound and ub is upper bound.since here is no inequality constraints or equality constraints, A,b,Aeq,beq are set as [],[],[],[],lb,up.

Then we execute the loop we will get different local maximum with bounded input. But, still this is not correct global maximum. to overcome that problem we need to increase the population size.

Time taken for study 2 :

Study 3 : Bounded inputs-Increasing population size :

To overcome this problem we need to increase the population size as it increases the probability to converage to a global maximum. The syntax that needs tobe used is as follows

[input,fopt]=ga(function,number of variables,[],[],[],[],lb,ub,[],[],options)

here by using the options we need to increase the population size. we here increases the population size to 500.

And by see the time taken for evaluate the global maximum is in this perticular study3 is about 35 sec which is larger than the study1 and study2.

Time taken for study 3 :

References :

     1) https://uk.mathworks.com/help/gads/ga.html

     2) https://in.mathworks.com/help/gads/what-is-the-genetic-algorithm.html

Conclusion : 

     By this program we understand about genetic algorithm and information regarding salagmite function and ways to optimize it. And from the study1, study2 and study3 we understand way to get the global maximum for this perticular salagmite function.